HIGH PERFORMANCE SCIENTIFIC COMPUTING
Modern, massively parallel computers play a fundamental role in a large number of academic and industrial applications and also constitute an integral part of the B3DCMB project. The need for this is driven by rapidly increasing data sizes and complexity of problems arising in different contexts. In the case of the B3DCMB project this is due to constant need for better sensitivity which is necessary to reach new sets of progressively more demanding science goals. This in turn unavoidably leads to a rapid increase of volumes of the data, what on its own requires better numerical tools capable to process those efficiently. Concurrently, however more advanced data models are needed to account for progressively smaller effects of different origins and which may imply more advanced algorithms which typically entail more involved computations.
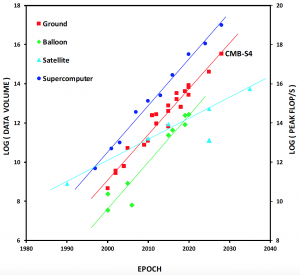
To address those new emerging problems what is necessary are (1) better numerical algorithms, and, (2) their better implementations suitable for hardware of the modern supercomputers. While the formal power of the supercomputers has been constantly growing, keeping up with the Moore’s Law, this has been happening at the cost of progressively increasing complexity of the computer hardware. Consequently, while the present-day supercomputers are as powerful as never before, their very complex, heterogeneous hardware architectures, effectively prevent most of the existing algorithms to scale up to a large number of processors, and thus capitalizing on their formally available power is becoming prohibitively daunting. To address this growing disparity we need better numerical algorithms, but better not only in the sense of merely leading to fewer floating point operations (FLOPs) but also in the sense of being more amenable to efficient implementation on those complex architectures of current and future supercomputers. This clearly rises stakes up !
One trend in hardware of modern supercomputers, which seems particularly consequential, is the exponentially increasing divide between the time required to communicate a floating-point number between two processors and the time needed to perform a single floating point operation by one of the processors. The slow rate of latency improvement is mainly due to physical limitations, and it is not expected that the development of the hardware will find a solution to this problem soon. The communication problem therefore needs to be addressed directly at the mathematical formulation and the algorithmic design level. This requires reconsidering the way the numerical algorithms are devised, which now need to reduce, or even minimize when possible, the number of communication instances. This realization led to an advent of the so-called communication avoiding algorithms which strive to minimize provably communication in numerical linear algebra (Demmel, Grigori, Hoemmen and Langou, 2012).
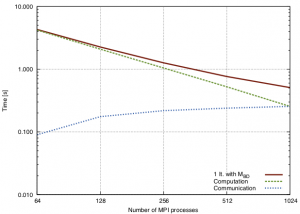
The communication gap is already seen and felt in the current, highly optimised applications, including those typical of the CMB field. This is due to the inherent specificity of the CMB data analysis, where the fully or nearly full data sets need to be processed simultaneously, what calls for massively parallel computational platforms and complex communication patterns (Sudursan et al, 2011, Cargamel, Grigori, Stompor 2013). It is illustrated in the figure on the right, which displays the performance of a linear solver based on iterative methods used in the cosmic microwave background (CMB) data analysis application. This performance result (see the original paper [Grigori, Stompor & Szydlarski 2012] for a detailed description of the experiment) shows the cost of a single iteration of conjugate gradient iterative solver preconditioned by a block diagonal preconditioner, together with the time spent on computation and communication. One can see that the communication becomes quickly very costly, potentially dominating the runtime of the solver when more than 1000 MPI processes are used (each MPI process uses 4 cores and 6 openMP threads per each core).
Another trend is the proliferation of the so-called accelerators. Indeed, some of the largest currently available and forthcoming common-user supercomputers commonly capitalize on the performance of general purpose graphic processing units, GPGPUs. This unavoidably adds yet another layer in already complex architecture of the supercomputers typically involving distributed and shared memory layer. Capitalizing on all these structure is the must if we want to maintain the performance of our codes with respect to the peak performance of the computers. The next generation of the codes will thus have to combine efficiently distributed, shared and GPU libraries and programming languages. The computational efficiency of the accelerators will further exacerbate the communication gap problem, even if the new generation of GPGPU is expected to allow for much more efficient communication between the CPU and GPU.
The new computer hardware will require new numerical algorithms and their implementation to ensure that their formal computing power is indeed capitalized on. New algorithms are needed also in order to improve the computational complexity and codes of the current approaches. In the context of the B3DCMB project we identified two major linear systems solutions of which constitute major part of the computational cost of the entire data analysis effort. These two systems are referred to as map-making and Wiener-filter systems, see, e.g., Papez et al (2018). These systems are commonly solved using iterative techniques, given that system matrices typically appearing in these problems can not be typically not only inverted but even constructed.

While the current techniques are often very efficient, if the new CMB data sets are to be analyzed still better algorithms are needed !
The B3DCMB project aims to address comprehensively these challenges in all their aspects !

